в этой статье мы узнаем, как сравнивать цифры

Выполнила Шадрина Наталья Дмитриевна,

учитель начальных классов

МБОУ СОШ № 24 им. Бутаева К. Владикавказ

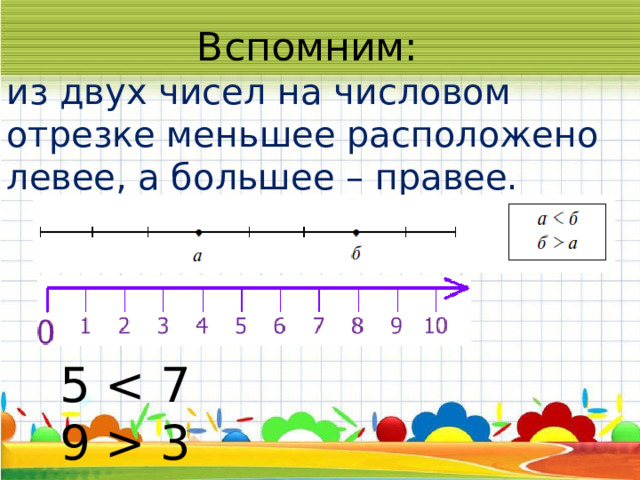
из двух чисел на числовом отрезке меньшее расположено левее, а большее – правее.

Нарисуем графические модели и сравним числа

Любое двузначное число больше, чем однозначное, и наоборот.

5 24 45 8

9 15 71 5

При сравнении двузначных чисел нужно начинать сравнивать десятки.

4 5, так как 6 д. 4 д. Сравним числа 7 5 2 4 4 5 8 8 8 9 1 5 5 1 7 2″ width=”640″

Число больше то, в котором десятков больше.

6 2 4 5, так как 6 д. 4 д.

Когда сравниваем двузначные числа, сначала сравниваем десятки ; если десятки равны , то сравниваем единицы.

Число больше то, в котором единиц больше.

7 5 7 4 4 5 4 8

7 9 7 5 7 1 7 6

Вспомним: 1 дм = 10 см

второе
полугодие

Учитель начальных классов
ГБОУ Школа №1222 имени маршала И.Х.Баграмяна г. Москвы
Луковкина Татьяна Сергеевна

Считаем устно
Назовите пропущенное число:

Какое число называют при счете

Назовите числа, которые стоят между

Назовите предыдущее
и последующее число:

Не решая примеров, скажите, где ответ больше или меньше? Почему?

Назовите самое маленькое
и самое большое число

Задание для самоподготовки
в тетради

У меня всё
получилось!

Не всё получилось,
но я старался.

Не старался,
Многое не получилось.

В.Н. Рудницкая Математика, 1 класс, учебник для учащихся общеобразовательных учреждений в 2 ч. Москва Издательский Центр «Вентана – Граф», 2015 г. ; часть вторая стр. 84, 86-87.
Печатная тетрадь Н.В. Рудницкая «Математика.1 класс. № 3», Издание: 4-е изд., перераб. – М.: Вентана – Граф, 2015; с. 58-60.

Продолжим тему обучения счету дошколят и в этой статье поговорим о сравнении смежных чисел, то есть об определении какое из смежных чисел меньше, а какое больше.

Ранее мы говорили об обучении ребенка счету, прибавляя и отнимая от чисел по единице. Теперь закрепим этот материал, научив ребенка определять, какое из смежных чисел больше или меньше.

Ребенок, в результате наших занятий, должен понять, что понятия больше и меньше относительные и что каждое число, кроме единицы, всегда больше или меньше другого числа. Это зависит лишь от того, что с чем сравнивают.

Например, 2 > 3, но 3 < 4.

При этом прививаем ребенку понятия, на сколько больше и на сколько меньше.

То есть 2 > 3 на 1.

Игра – сравнение 1

Для этой игры нам понадобится набор шашек. Выставим на шахматное поле шашки рядами таким образом: первый ряд 1 шашка белого цвета, под ней второй ряд – 2 черных шашки, под вторым третий ряд – 3 белых шашки, под ним четвертый ряд – 4 черных и так далее.

Покажем ребенку, что шашек в каждом ряду больше чем в предыдущем, но меньше чем в последующем ровно на одну фигуру. Теперь покажите ребенку, что для того, чтобы в любом ряду стало фигурок столько же, сколько в ряду к верху от него надо, надо убрать одну шашку, а к низу – добавить шашку. Теперь выберите ряд, и пусть ребенок сам покажет вам, где шашек больше, чем в этом ряду, а где меньше.

Цель следующей игры не только научить сравнивать смежные числа, но также показать независимость размера предметов от их количества.

Игра – сравнение 2

Для этой игры нам понадобится 6 – 7 кружков большого размера диаметром 7 см и столько же кружков меньшего диаметра, допустим 5 см.

Разложим кружки на две группы с одной стороны 4 большего диаметра, а с другой стороны 5 меньшего. Сосчитайте кружки в обоих группах вместе с ребенком, указывая ему на то, что сравнить количество кружочков можно не зависимо от их размеров. Теперь добавьте кружочек в группу с большим диаметром. Попросите ребенка посчитать и сравнить количество. Спросите, равно ли количество кружочков в группах. Таким образом, вы покажите ребенку, что количество предметов не зависит от их размеров.

Урок путешествие в сказочную страну «Матаматика»

Тема: Сравнение чисел.

Цель: Формировать умения сравнивать число.

Создать условия для формирования умения сравнивать числа.

Создать условия для развития наблюдательности, внимания,

математической речи, мыслительных операций у учащихся.

Способствовать воспитанию дружеских взаимоотношений,

взаимопонимания, умения работать друг с другом; воспитанию интереса к

Оборудование: тетрадь, книги, презентация.

Тип урока: изучение нового материала.

– Прозвенел звонок – начинается урок. Пусть сегодня на уроке царит тёплая

Мы пришли сюда учиться, не лениться, а трудиться.

Слушаем внимательно, работаем старательно.

Мы приветствуем гостей, дорогих учителей.

Всех знакомых, незнакомых, и серьёзных, и весёлых.

И сегодня 1 класс на урок позвал всех вас.

– Садитесь, посмотрите на экран. Сегодня у нас не обычный урок-

путешествие, а путешествовать мы будем по сказочной стране , которая

называется «Математика» , путешествие будет проходить по плану:

1 этап. Настроимся

2 этап. Что мы знаем

3 этап. Изучаем,

4 этап. Закрепляем

5 этап. Подводим итоги.

– Первый этап позволит нам настроиться на работу.

Второй этап – покажет, что мы знаем.

На третьем этапе мы получим новые знания.

А на четвёртом – закрепим их.

На пятом – подведем итог урока.

Устный счет: ( 1 этап настроимся)

-Сейчас время года зима, поэтому и устный счет у нас называется зимняя

7+2 =9 7-2=5 6+2=8 10-2=8 6+4=10

9-3=6 5+3=8 8-3=5 6+3=9 10-3=7

7-3=4 9-3=6 7+3=2 9-4=5 5+4=9

Повторение ( 2 этап, Что мы знаем)

-Что такое десяток? (счетная единица равная 10)

-Как по-другому можно назвать 10 единиц? (десяток)

-Чему равен десяток? (10 единиц)

– Прочитайте числа в порядке убывания : 90, 100, 10, 70,40, 20, 50, 60, 80,30.

-Прочитайте числа в порядке возрастания: 70, 30, 20, 40, 100, 60, 50,

Изучение нового материала: (3 этап)

Откройте тетради, запишите число, в классе.

Сегодня на уроке мы будем учиться сравнивать числа, а точнее десятки.

Ребята, посмотрите на доске записаны числа нам нужно сравнить их, для

этого мы будем использовать слова, «больше», «меньше», «равно» и знаки

«˃» , «˂», «=».

5 дес. * 9 дес.

Чтобы сравнить, мы с вами будем обращать внимание на количество

десятков, т. на цифру перед словом десяток.

Давайте сравним, какое число больше 5 или 9? (9), значит 9 десятков больше,

чем 5 десятков, ставим подходящий знак:

5 дес. ˂ 9 дес.

А сейчас мы переведем, 5 десятков- 50, 9 десятков -90

50 ˂90

Для того чтобы сравнить числа, мы закроем нули, что больше 5 или 9, (9)

Значит число 90 больше, чем 50.

2 дес. +3 дес. * 6 дес – 2 дес.

А чтобы решить такие выражения нам сначала нужно решить, какое число

получится в правой части, подписываем полученное число сверху

карандашом, затем решить левую часть подписать число, а когда мы знаем

числа мы можем сравнить.

-Сколько получилось в правой части? ( 5 дес

-Сколько получилось в левой части? (4 дес

-Какое число больше ? (5 десятков)

Значит 2 дес. +3 дес. Больше, чем 6 дес – 2 дес. , ставим знак больше «˃»

Переведем в числа:

20+30 60-20,

Чтобы сравнить, мы посчитаем, какое число получится в правой части, и

какое в левой.

Закрываем нули, 2+3=5 в правой части число 5, в левой закрываем нули,

считаем, 6-2=4, мы с вами нашли числа,

-Какое число больше? (5)

Повторение, вторичное проговаривание.

Закрепление: (4 этап)

Страница 167, №3

4дес. ˃ 1 дес. 3 дес. +1дес. ˃4 дес. -1дес.

40˃10 30+10˃40-10

7 дес. ˃5 дес. 9дес. – 3 дес. = 4 дес. +2 дес.

70˃50 90-30=40+20

Мы хлопаем в ладоши, хлоп, хлоп

хлопки над головой

Мы топаем ногами, топ, топ

высоко поднимаем колени

головой вперед назад подвигать

Мы руки поднимаем, мы руки опускаем

руки поднять, опустить

Мы низко приседаем и прямо мы встаем

присесть и подпрыгнуть

Руки вниз, на бочок.

Разжимаем- в кулачок

Руки вверх и в кулачок

Разжимаем на бочок

На носочки поднимайся

Приседай и выпрямляйся

Ноги вместе. ноги врозь

Страница 167, №4

Придумайте задачу по схеме и краткой записи.

У Даны -?, на 3 больше.

У Маржан 7 ручек, у Даны -?, на 3 больше. Сколько ручек у Даны?

-О чем говорится в задаче? (о ручках)

-Что известно в задаче? (У Маржан 7 ручек, у Даны-?, на 3 больше.

-Что нужно найти ? ( Сколько ручек у Даны?)

-Какие слова возьмем для краткой записи? (У Маржан 7 ручек, у Даны-?, на 3

Какое действие выберем?(Сложение) Почему? (потому что больше)

Предмет: Математика.

Класс: 4 «А».

Тема урока: Сравнение многозначных чисел.

Цель урока: Учить сравнивать числа, состоящие из единиц I и II классов; совершенствовать устные и письменные вычислительные навыки.

образовательная: повторить умения читать и записывать многозначные числа, рассмотреть способы сравнения многозначных чисел;

развивающая: развивать приемы логического и алгоритмического мышления, сравнения, аналогии;

воспитательная: воспитывать ответственное отношение за результат своего труда.

Средства обучения: учебник математика М. Моро.

Сегодня
мы поговорим о том, как сравнивать многозначные числа. В нашей
жизни часто приходится сравнивать разные числа. Вот, допустим, пришли вы в
магазин, имея определённую сумму денег. Для того, чтобы быть уверенным, что ваших
денег хватит на оплату покупки, вы должны сравнить количество денег, которое у
вас есть у вас денег и стоимость товаров, которые хотите приобрести. А как же
научиться сравнивать числа?

Посмотрите
на числовой луч.

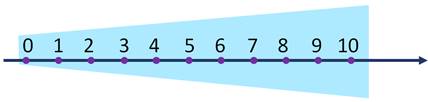
Ещё
в первом классе вы познакомились с тем, что числа на нём расположены в порядке
возрастания. Из двух чисел меньше то число, которое на луче находится
левее, и при счёте его называют раньше. И больше то число, которое на
луче находится правее, и при счёте его называют позже. Три меньше четырёх, а
четыре больше трёх. Пять меньше девяти, а девять больше пяти.

А
вот если надо сравнить числа девять и одиннадцать. Сравнить эти числа можно
двумя способами. Первый – тот, о котором мы только что говорили. Число девять на
луче находится левее одиннадцати, и при счёте его называют раньше одиннадцати,
значит, девять меньше одиннадцати, а одиннадцать – больше девяти

Но
есть и ещё один способ сравнения чисел. Число девять –
однозначное, то есть записано одной цифрой. А число одиннадцать – двузначное,
записано двумя цифрами.

При
сравнении чисел большим будет то число, в котором больше цифр. Триста пятьдесят четыре больше сорока двух. Семь тысяч пятьсот меньше
семнадцати тысяч пяти.

А
теперь сравним числа двести шестьдесят восемь и четыреста девятнадцать. Они оба
трёхзначные и на луче они не стоят рядом, поэтому сравнить их по месту
нахождения на числовом луче и по количеству цифр мы не можем. Сравнивать их мы
будем поразрядно. Начинаем сравнение с высшего разряда. В
этих двух числах такой разряд – сотни. Две сотни меньше четырёх сотен. Дальше
эти числа сравнивать не надо. Большим будет то число, в котором больше единиц
высшего разряда. Значит, двести шестьдесят восемь меньше четырёхсот
девятнадцати.

Сейчас
мы сравним числа две тысячи семьсот девятнадцать и две тысячи шестьсот сорок
восемь. Высший разряд в обоих числах – единицы тысяч. И в одном, и в другом
числе они одинаковы – две тысячи. Сравниваем следующий разряд – сотни. В числе
две тысячи семьсот девятнадцать – их семь, а в числе две тысячи шестьсот сорок
восемь – их шесть. Семь больше шести, значит и всё число две тысячи семьсот
девятнадцать больше числа две тысячи шестьсот сорок восемь. Мы уже знаем ответ,
и сравнивать дальше эти числа не имеет смысла.

А
теперь давайте попробуем сравнить числа пятьдесят три тысячи двести семьдесят
три и пятьдесят три тысячи двести тридцать семь.

Так
как числа большие, многозначные, начнём с того, что разобьём эти числа на
классы, отделив справа три цифры класса единиц. Так удобнее определить,
равное или нет у них количество цифр. Вот теперь мы прекрасно видим, что оба
эти числа – пятизначные. При счёте они не стоят рядом, поэтому сравнить их по
месту нахождения на числовом луче не получится. Конечно, нам придётся
сравнивать эти числа поразрядно, начиная с высшего разряда. Сейчас оба числа я буду записывать в таблицу классов и разрядов. Так удобнее будет их сравнивать.

В
числе пятьдесят три тысячи двести семьдесят три – пять десятков тысяч, и в
числе пятьдесят три тысячи двести тридцать семь тоже пять десятков тысяч. В первом
числе три единицы тысяч, и во втором тоже три единицы тысяч.

Сотен
и в первом числе и во втором по две. А десятков. В первом числе их семь, а во
втором – три. Стоп. Этого достаточно. В обоих числах равны разряды десятков
тысяч, единиц тысяч и сотен. Но большим будет то число, в котором больше
десятков. Количество единиц при этом уже значения не имеет. Хотя конечно, их мы
тоже запишем.

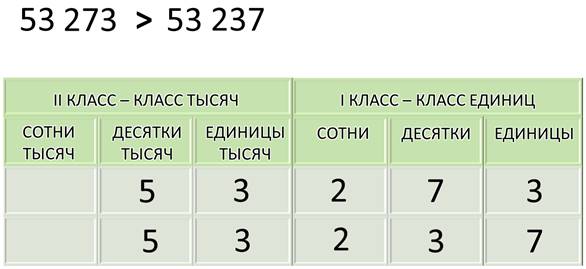
Я
записала эти два числа в таблицу, потому что так вы более наглядно можете
увидеть последовательность поразрядного сравнения многозначных чисел.

Ну
что же, пришло время повторить всё то, что мы сегодня говорили.

Числа
можно сравнивать разными способами:

Способ
первый. Сравнение по расположению на числовом луче.

Из двух чисел, которые размещены на луче, больше то число,
которое расположено правее, и меньше то, что стоит левее.

Способ второй. Сравнение по количеству разрядов.

Больше то число, в котором больше разрядов.

При этом проверять количество единиц в каждом разряде не
надо.

Если разрядов в числах одинаковое количество, переходим к
третьему способу – сравниваем количество единиц в каждом разряде, начиная с
высшего.

Способ третий. Сравнение по разрядам.

Если число многозначное, выполняем сравнение по следующему алгоритму:

Разобьём число на классы

Количество цифр разное? Если да, то большим будет то число, в
котором больше цифр. Сравнение чисел закончено.

Если количество цифр одинаковое, то сравниваем значения
высшего разряда.

Эти значения разные? Если да, то большим будет то число, в
котором значение разряда больше. Сравнение закончено.

Если значения одинаковые, то сравниваем значения следующего
разряда.

А если значения одинаковые, то сравниваем значения следующего
разряда.

И так продолжаем до тех пор, пока не появятся разные значения
какого-либо разряда. А теперь попробуйте сами сравнить числа,
пользуясь всеми этими способами.

Вы
готовы? Давайте проверим вашу работу. Надеюсь, вы были внимательны и сравнили
числа правильно.

Первую
пару чисел можно было сравнить по количеству разрядов в них. В
числе шестьдесят тысяч пятьсот двадцать четыре их меньше, чем в числе семьсот
девять тысяч триста шестнадцать. Поэтому там стоит знак меньше.

Во
второй паре количество разрядов одинаково, но сравнить достаточно
было только высший разряд. Так как пять больше четырёх, то и всё
число пятьсот тридцать шесть тысяч двести сорок девять больше числа четыреста
семьдесят восемь тысяч девятьсот шестьдесят девять.

В
третьей паре чисел надо было сравнивать все разряды, начиная с
высшего, до разряда десятков в классе единиц.

Ну,
вот и пришло время нам сегодня прощаться. Продолжайте работать сами. Будьте
внимательны. До новых встреч!

УМК: “Начальная школа XXI века”.

используя слова “выше”, “ниже”, “дороже”, “дешевле” продолжать формирование навыка сравнения чисел и предметов;
закреплять навыки сравнения предметов по цвету, форме, размеру;
воспитывать интерес к изучению математики.

Оборудование: учебник, рабочая тетрадь, наборы картинок (солнышко, тучки), цветные карандаши, проектор, экран, компьютер, презентация.

Ход урока

МАОУ “Школа №125”

Тема урока: «Сравнение
чисел» (6 класс, А. Мерзляк)

Тип урока: урок открытия нового знания

Форма занятия: исследовательская деятельность
обучающихся

· познакомить
с правилами сравнения положительных и отрицательных чисел;

· учить
применять полученные знания при выполнении различных заданий.

· способствовать
овладению учащимися основными способами мыслительной деятельности
(умение сравнивать, анализировать, делать выводы);

· способствовать
развитию математической речи учащихся.

· способствовать
формированию познавательного интереса;

· способствовать
формированию личностных качеств: доброты, взаимопомощи, милосердия,
умения слышать и слушать, работать в парах и группах.

Предметные: знать правила сравнения чисел, решать
задания на сравнение рациональных чисел.

Метапредметные: умение выдвигать гипотезы, предположения,
анализировать, сравнивать, видеть различные способы решения задачи.

Личностные: умение правильно излагать свои мысли,
понимать смысл поставленной задачи, работать в паре и группе; излагать и
аргументировать свою точку зрения; оценивать себя и товарищей.

-Добрый день, ребята!

-Эпиграфом к нашему уроку станут следующие слова «Единственное
счастье в жизни – это постоянное стремление вперед» (Слайд 2)

-Как понимаете эту цитату? (Обсуждение)

Актуализация знаний (3-4 мин)

-Сделать новые открытия для себя мы сможем лишь при условии
закрепления прежних знаний и умений. Поэтому давайте вспомним то, что уже
знаем. Как называется глава, с которой мы начали знакомиться? И конечно же
вспомним действия с ними. На слайдах презентации будут представлены для вас
задания. (слайды4-5 ).

Подготовка
к усвоению нового материала. Создание пробл ситуации (2-3 мин)

– В последних двух строчках возникло затруднение. Почему мы не
можем сравнить их? Как называются эти числа? Все ли числа мы умеем сравнивать?
Тогда сформулируйте тему и цели урока (слайды
6).

III. Работа
в группах. Изучение нового материала (8-10 минут)

– А теперь что бы достигнуть
этих целей объединитесь в группы. Каждая группа получает свой мини – проект на
исследование правила сравнения. Исследование осуществляется по заданному
алгоритму. Пользуясь им, вы его выполняете. А потом защищаете свой проект
“Правила сравнения”. Ваша задача в течении 5-6 минут (слайд
7)

1
группа – Вывести правило сравнения положительных и отрицательных чисел.

2
группа – Вывести правило сравнения двух отрицательных чисел.

3
группа – Вывести правило сравнения положительных, отрицательных чисел и
нуля.

– Капитаны групп пройдите к доске и доведите до нашего сведения
результат вашего исследования. ( слайд 8)

Ø Любое
положительное число больше любого отрицательного числа.

Ø Из
двух отрицательных чисел
меньше то, модуль которого больше.

Ø Любое
отрицательное число меньше нуля, любое положительное число больше нуля

– На сколько вы нас убедили,
проверим сейчас на примере. Каждой группе задание приведите свой
пример.

-И так, результатом нашего
исследования стали правила сравнения: правила зачитать из учебника (Сравнить
свои правила с правилами из учебника стр. 197)

Работа
с учебником.

Закрепление полученных
знаний №920,921,923 (приложение 1).

– Молодцы! Вы, наверное, устали? Давайте, немного
отдохнем! Ребята, если число положительное, то поднимаем руки вверх, если
отрицательное, то приседаем. Итак, начали:

-Дальше работаем со следующей
таблицей. (11 слайд) Для того, чтобы расшифровать слово
вам необходимо расставить числа в порядке возрастания. Затем заменить каждое
число буквой. У вас должно получится слово.

Историческая справка. Брахмагупта
– индийский математик, который жил в VII веке. (Слайд
12)

Одним из первых он
начал использовать положительные и отрицательные
числа. Положительные числа он называл
«имущество», отрицательные – «долги».

-Молодцы!
Продолжим свою работу. Проверим, как вы усвоили
новый материал, выполнив небольшое тестирование. На столах у вас лежат
листы достижения, результаты вносите в таблицу. Не забудьте подписать их. Если
задание выполнено верно ставим знак «+» , не верно «-». Проверяем по
слайдам.

Укажите верное неравенство. (10 слайд) 1)-5>2;

Укажите неверное неравенство. (11 слайд) 1)4>0;

Расположите числа -100, -200 и 50 в порядке возрастания (12
слайд)

2)50, -100, -200;

Укажите наименьшее число. (13 слайд) 1)
-13,97;

Сколько целых чисел удовлетворяют неравенству. (14
слайд)

-8 < х< 4?

VII. Подведение
итога.

-Как вы думаете, достигли ли
мы поставленных перед нами целей? Научились ли мы сравнивать числа? Давайте
подведем итог.

Положительное число всегда
больше отрицательного.

Из двух отрицательных чисел
больше то, модуль которого больше.

Отрицательное число всегда
меньше нуля.

Положительное число всегда
меньше нуля.

VIII. Рефлексия.

–
Спасибо вам за урок!

Д/з. §
33 знать правила;, № 922.

(раздать готовые таблицы для заполнения) к примеру №923

(расположить
в альбомном варианте и распечатать)

Сравнение многозначных чисел с одинаковым количеством цифр

Чтобы сравнить $2$ числа, можно сравнивать их по разрядам, начиная с наивысших.

Сравним $2305$ и $2186$.

Сравниваем по очереди тысячи, сотни, десятки и единицы обоих чисел. Итак, тысячи тут совпадают (и там $2$, и там $2$), тогда смотрим на сотни.

В $2305$ — $3$ сотни, а в $2186$ — $1$ сотня. Значит, в $2305$ больше сотен, чем в $2186$, поэтому $2305 > 2186$.

Из двух чисел с одинаковым количеством цифр, больше то, у которого больше первая (слева направо) из неодинаковых цифр

Сравним $4910$ и $4909$. Сравниваем цифры слева направо:

Для удобства запишем эти числа одно под другим:

Итак, первые слева цифры у чисел — это четвёрки. Значит, сравниваем следующие цифры. Далее идут девятки. Значит, сравниваем следующие. И так будем сравнивать до тех пор, пока сравниваемые цифры не будут разными.

Смотрим далее — у первого числа стоит $0$, а у второго в этой позиции — $1$. $1$ больше, чем $0$, значит, и второе число больше, чем первое.

Натуральный ряд чисел и сравнение чисел

Образавр и Вообразавр решили поспорить, кто за пять минут сделает больше самолетиков из бумаги. Чтобы помочь им, давайте разберемся, как сравнивать натуральные числа. Ведь именно так, посмотрев на результат соперника, можно увидеть, кто пока выигрывает.

Вспомним, что все натуральные числа образуют натуральный ряд чисел:

В этом натуральном ряду каждое следующее число на единицу больше, чем предыдущее. Или каждое следующее число получается прибавлением к предыдущему единицы.

Так, $4$ на единицу больше, чем число $3$. А если к $9$ прибавить $1$, получится следующее число — $10$. И так с каждой парой соседних чисел в ряду натуральных чисел.

Из двух натуральных чисел больше то, которое в ряду натуральных чисел стоит правее (дальше от начала).

Это означает, что чем дальше от начала находится число в ряду натуральных чисел, тем оно больше.

Например, число $13$ больше числа $9$, число $9$ больше числа $5$, так как в ряду натуральных чисел число $13$ находится правее числа $9$, а $9$ правее числа $5$.

И наоборот, число $9$ меньше числа $13$, число $5$ меньше числа $9$, так как в ряду натуральных чисел, число $9$ находится левее числа $13$, а $5$ левее числа $9$.

Если одно число больше или меньше другого, то в математике это называется неравенством.

Но это лишь один из способов. Выделяют и другие. Например:

Одно число больше другого, если его при счете произносишь позже, а меньше, соответственно, то, которое называешь раньше.

Сравнить числа $9$ и $13$ легко, потому что числа небольшие и легко понять, какое из них будет находиться в ряду правее, и какое левее.

А если числа, которые нужно сравнить, большие, состоят из трех и более цифр? Такие как $648$ и $7352$, или $340567$ и $341974$. Каким образом выяснить, какое из чисел будет больше? Для этого нужно посмотреть, из скольких цифр состоят числа.

Из двух чисел больше то число, у которого цифр больше.

Рассмотрим еще один пример. Допустим, у нас есть числа $2, 876, 63, 20987, 7774, 109453$. И нам нужно расположить их по возрастанию, то есть от самого маленького до самого большого. Обратим внимание, из скольких цифр состоит каждое число:

Значит, самым маленьким будет число из одной цифры — это число $2$. Далее будет число, состоящее из двух цифр — это число $63$. Следующее состоит из трех цифр — число $876$. Затем из пяти цифр — $20987$. И самым большим будет число, которое состоит из $6$ цифр — $108453$.

Двойное неравенство

С простым неравенством разобрались, но в математике выделяют ещё и двойное, то есть, когда сравнивают уже не $2$, а $3$ числа. Соответственно, в таком случае уже не $1$ знак, а $2$. Давайте разберёмся. Выделяют несколько особенностей, сравнивая $3$ числа.

Во-первых, самое главное из них — то число, которое стоит посередине. Мы только с ним сравниваем $2$ других. Например, пять больше двух, но меньше восьми ($2<5<8$). Мы с числом $5$ сравниваем числа $2$ и $8$, но обязательно по очереди. Сначала берем число, находящее слева, а потом уже другое.

Во-вторых, всегда одинаковые знаки. Если вначале поставили «$<$», то и второй знак будет точно таким же.

Хотя знаки в двойном неравенстве одинаковые, произнося ответ, мы всегда должны где-то употребить слово «больше», а где-то «меньше». Как правило, сначала употребляют слово «больше», а потом «меньше» ($5$ больше $2$, но меньше $8$).

Рисунок 4. Чтение неравенств

Свойства неравенств

Неравенства подчиняются общим правилам, которые называют свойствами неравенств. Давайте разберем некоторые из них.

Если первое число больше второго, а второе больше третьего, значит, первое число больше третьего, то есть если $a > b$, а $b > c$, то $a > c$

Чтобы было понятнее, давайте подставим вместо букв числа. Пусть $a = 5$, $b = 3$, $c = 2$.

$$5 > 3$$

$$3 > 2$$

$$5 > 2$$

Если к обеим частям неравенства прибавить одно и то же число, то неравенство не изменится, то есть если $a > b$, то $a +c > b + c$

Проверим на числах:

$$5 + 2 > 3 + 2$$

А как вы думаете, что будет больше, $a + b$, $a-b$ или $a$?

Если числа $a$ и $b$ являются натуральными, то $a + b > a$. Проверим:

$$5 + 3 > 5$$

Ну а $a-b$ будет меньше, чем $a$.

$$5-3 < 5$$

Строгие и нестрогие неравенства

Те неравенства, которые мы разбирали выше, называются строгими. Помимо них, в математике также есть нестрогие неравенства. Они обозначаются знаками $leq$ и $geq$.

Рисунок 3. Знак нестрогого неравенства

Пример нестрогого неравенства: $n leq m$

Что это значит, как думаете?

Это значит, что число $n$ либо $<$, либо $=$ числу $m$.

Данное неравенство нужно читать так: «$n$ меньше или равно $m$».

Иначе можно было бы записать то же самое так: $n < m$ или $n = m$

Получается, что неравенство $n leq m$ удовлетворяет одно из двух условий.

Нестрогое неравенство является верным в случае, если выполняется хотя бы одно из двух его условий, то есть одно число либо равно сравниваемому с ним числу, либо больше или меньше его (в зависимости от знака).

Например, давайте рассмотрим нестрогое неравенство $7 geq 6$. Является ли оно верным?

Да, так как одно из его условий выполняется: $7 > 6$

А будет ли верным неравенство $7 geq 7$, как думаете?

Тоже да, так как $7 = 7$. Одно из условий выполняется.

А вот нестрогое неравенство $7 leq 6$ не является верным, ведь ни одно из его условий не выполняется.

Конспект урока математики “Сравнение чисел” в контексте ФГОС НОО

подробный конспект урока по данной теме. Технологическая карта.

Содержимое разработки

Конспект урока математики в 1 «Б» классе

Тема: «Сравнение чисел »

Тип: урок изучения нового материала.

Цель урока: сформировать знания и умения учащихся по теме «Сравнение чисел».

учить сравнивать числа, выражая результат сравнения словами «больше», «меньше»;
развивать познавательный интерес, умение наблюдать, обобщать, делать выводы, развивать регулирующий компонент учебной деятельности – самоконтроль и взаимопроверку;
воспитывать положительную мотивацию в обучении, стремление использовать математические знания в повседневной жизни;

Планируемые метапредметные результаты

Личностные: проявлять способность к самооценке на основе критерия успешности учебной деятельности, уважительное отношение к собеседнику.

Познавательные: уметь ориентироваться в своей системе знаний: находить ответы на вопросы, используя учебник, информацию, полученную на уроке.

Регулятивные: уметь определять и формулировать цель на уроке с помощью учителя; планировать свои действия в соответствии с поставленной задачей.

Коммуникативные: уметь с достаточной полнотой и точностью выражать свои мысли, слушать и понимать речь других; учиться работать в парах, формулировать собственное мнение.

Планируемые предметные результаты: знать правила сравнения чисел; уметь сравнивать числа, решать примеры на сложение и вычитание чисел в пределах 20.

Организация пространства: фронтальная, индивидуальная, парная работа.

Методы: объяснительно – иллюстративные, частично-поисковые, словесные, практические.

Оборудование к уроку:

-учебник (Рудницкая В. Математика: 1класс: учебник. – М. : Вентана-Граф,2011);

-рабочая тетрадь (Математика: 1класс: рабочая тетрадь / В. Рудницкая – М. : Вентана-Граф,2011);

-сигнальные карточки, карточки для индивидуальной работы;

-демонстрационный материал (картинки)

№ Этапы урока Деятельность учителя Деятельность учащихся Формируемые УУД 1. Организационный момент. Цель, которая должна быть достигнута обучающимися:подготовиться к продуктивной работе на уроке. Цель, которую учитель хочет достичь на данном этапе:- создание условий для возникновения у обучающихся внутренней потребности включения в учебную деятельность. Задача:- создать положительный настрой;Методы: словесные, объяснительно – иллюстративные. ( – Ребята, сегодня у нас на уроке много гостей. Повернитесь и поприветствуйте их ) Вот звонок нам дал сигнал, Поработать час настал. Даром время не теряем И работать начинаем. А теперь проверь, дружок: Ты готов начать урок? Всё ль на месте, всё ль в порядке- Ручка, книжка и тетрадка?- Ребята, покажите, пожалуйста, с помощью карточек-смайликов, с каким настроением вы начинаете этот урок. Я думаю, что такое же приподнятое настроение будет у всех и в конце урока. – Продолжить наш урок я хотела бы словами: «Если человек за день не получил никаких знаний, значит день прошёл зря». Давайте дадим себе установку, чтобы наш урок прошёл не зря. Какую цель поставим перед собой?- Я желаю вам успешной и плодотворной работы. Дети тихо садятся на местаДети проверяют готовность к урокуПоднимают карточки-смайлики- Получить новые знания Личностные УУД: готовность к обучению, положительное отношение к учению. Регулятивные УУД:прогнозирование предстоящей работы. Коммуникативные УУД:развивать умение строить речевое высказывание. АБВ Изучение учебного материала. Актуализация опорных знаний. Цель, которая должна быть достигнута учащимися: продемонстрировать знание состава чисел; умение считать числа от 1 до 20 в прямом и обратном порядке, выявлять закономерность образования числового ряда. Цель, которую хочет достичь учитель:- актуализировать личностный смысл обучающихся к изучению темы;- организовать выполнение обучающимися пробного учебного действия. Методы организации работы: словесные. Постановка учебной задачи. Цель: обсудить затруднение и сформулировать цель урока. Открытие новых знаний:Цель: обсудить проект решения учебной задачи и вывести правила сравнения чисел без опоры на рисунок. Методы: учебный диалог, моделирование. – Ну а начнём мы с устного счёта. Посчитайте по цепочке от 1 до 20 в прямом и обратном порядке. А теперь через одно число. Прочитайте ряд чисел, записанный на доске. Определите закономерность образования ряда чисел. Продолжите этот ряд до 19, не нарушая закономерности. Какие числа пропущены?- Вспомним состав чисел. Заполните пустые окошки в числовых домиках. – Давайте сравним количество слоников и цыплят. Кого больше? Как сравнить предметы?- Образуйте пары картинок: слоник – цыплёнок. Кто остался без пары? Кого больше?- Итак, какой способ сравнения использовали?- А теперь давайте сравним количество учеников в нашем классе и в 1 «А». Где учеников больше, а где меньше? Как это сделать?- А в нашем классе нет ребят из параллельного класса?- В нашем классе 25 человек, а в 1 «А» – 12 человек. Где больше? Как это можно доказать?- Почему 25 больше 12? Как сравнить эти числа? В чём проблема?- Вы хотите решить эту проблему? Предположите, какой будет тема нашего урока? (на доске открывается тема урока)- Какую учебную задачу мы поставим на урок, чему должны научиться?- Откройте учебник на 84 странице. Рассмотрите внимательно рисунок и ответьте на вопросы. – Пересчитайте красные шары. Сколько их? Пересчитайте синие шары. Сколько их? Каких шаров меньше? Каких шаров больше? – А почему вы считаете, что синих шаров больше, чем красных, а красных меньше, чем синих? – Числа, ребята, можно сравнивать и без рисунков. Сегодня мы научимся это делать. – Посчитайте от 1 до 10. Какое число при счёте было названо раньше: 2 или 3? Это число большее или меньшее? Какое число при счёте было названо раньше: 8 или 9? Это число большее или меньшее? Какой можно сделать вывод?- Посчитайте от 11 до 20. Какое число было названо позже: 11 или 10? А это число большее или меньшее? Какое число было названо позже: 16 или 14? А это число большее или меньшее? Какой можно сделать вывод? Где мы можем проверить эти выводы? – Прочитайте правило на странице 84 в рубрике «Обрати внимание». Итак, как сравнить числа без рисунков? Считают -1, 4, 7, 10- Через два числа- 13, 16, 19- 2, 3, 5, 6, 8, 9, 11, 12, 14, 15, 17, 18Ученики выходят по одному к доске и вписывают числа в пустые окошки. – Составить пары Один ученик работает у доски – составляет пары картинок: слоник – цыплёнок. Ответы детей- Составление пар. – Составить пары из учеников нашего класса и 1 «А»- Нужно посчитать детей в нашем классе и в классе «А»- В нашем классе. 25 больше 12 -Мы не можем объяснить, почему 25 больше 12. – Да. – Сравнение чисел. – Как сравнивать числа. Открывают учебник, рассматривают рисунок, читают вопросы. – 3 -4 – Красных – Синих Варианты ответов детей: «- Это видно по рисунку», «- 4 больше 3, а 3 меньше 4», составить пары шариков: синий – красный, без пары останется синий шарик, значит, синих шариков больше, чем красных, а красных меньше, чем синих»Один ученик считает, остальные внимательно слушают. – 2; меньшее – 8; меньшее- Меньшее число при счёте мы называем раньше – 11; большее – 16; большее – Большее число при счёте мы называем позже. – Выводы можем проверить по учебнику. Читают правило. Регулятивные УУД:- развивать умение оценивать учебные действия в соответствии с поставленной задачей. Коммуникативные УУД:- развивать умение слушать и понимать других. Познавательные УУД:- ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя. Познавательные УУД:- постановка и формулирование проблемы- ориентироваться в своей системе знаний: отличать новое от уже известного с помощью учителя;Коммуникативные УУД: сотрудничество в поиске и сборе информации. АВ Закрепление учебного материала. Первичное закрепление с проговариванием во внешней речи. Цель, которую учитель ставит перед учениками:учиться сравнивать числа с помощью слов «больше», «меньше». Цель, которую ставит перед собой учитель: создать условия для формирования умения сравнивать числа без опоры на рисунок. Задачи:- развитие умений сравнивать два числа с помощью слов «больше», «меньше»;- развитие умений определять способ сравнения чисел;Методы: репродуктивные. Включение в систему знаний и повторение. Цель, которую ставит перед собой учитель: формировать навык применения изученных способов действийЗадачи:- развивать вычислительные навыки;- развивать способность давать адекватную оценку. – Можем ли мы теперь ответить на вопрос «Почему в нашем классе учеников больше, а в 1 «А» меньше? – Ребята, что ещё нам надо сделать, чтобы хорошо научиться сравнивать числа? Работа по учебнику. Выполнив задание №3, мы закрепим правило сравнения чисел: Какое число больше: 13 или 19, 20 или 15, 5 или 8? Объясните свой выбор. Какое число меньше: 11 или 14, 13 или 9, 17 или 20? Объясните свой выбор. – Рассмотрите рисунок на странице 85. Сколько огурцов собрала Маша? Сколько огурцов собрал мальчик Петя? Прочитайте вопрос и ответьте на него. Объясните свой ответ. – Давайте выполним задание № 8 со значком «Обсудим вместе». Прочитайте задание. Кто назовёт самое большое число. Какое число будет следующим? Значит это не самое большое число. Какое бы большее число вы не называли, всегда можно назвать следующее, которое при счёте идёт за этим числом, а значит, будет больше. Самого большого числа не существует. А самое маленькое? Для вас, мои маленькие первоклассники, самое маленькое число – это нуль. Физкультминутка. Буратино потянулся,Раз нагнулся, два нагнулся. Руки в стороны развёл,Ключик видимо нашёл,Чтобы ключик тот достать,Надо на носочки встать. Работа в тонких тетрадях. – Откройте тоненькие тетради. Запишите сегодняшнее число. При помощи каких цифр оно записано? Пропишите их. – Откройте учебник на странице 87. Решите примеры из № 16 по вариантам. Вариант 1 Вариант 2 5 + 6 11 – 3 7 + 5 10 – 4 6 + 8 15 – 6 9 + 6 13 – 5- Поменяйтесь тетрадями и проверьте работу друг у друга. Теперь сверьте с ответами на доске. (обговорить результаты – кто выполнил без ошибок, с одной ошибкой и т. ) – Сравните результаты сложения чисел в 1 варианте. Назовите наибольшее число, наименьшее. – Сравните результаты вычитания чисел во 2 варианте. Назовите наибольшее число, наименьшее. Индивидуальная работа по карточкам. – У вас на партах лежат карточки с заданиями. Выполните их. Сверьте ваши ответы с ответами на доске. Обведите в кружок красным карандашом большее число: 9 и 3; 7 и 10; 15 и 13 2. Обведите в кружок синим карандашом меньшее число: 2 и 5; 11 и 9; 18 и 13 3. У Наташи 10 марок, а у Димы 12 марок. У кого больше?__________________________ У кого меньше?___________________________ – Кто выполнил это задание без ошибок? Поднимите руки. У кого возникли трудности? Чему надо ещё поучиться? -Если вы считаете, что слабо умеете выполнять такую работу, нам нужно ещё потренироваться, поработать над этим, и я вам помогу. Работа в тетрадях на печатной основе. – Кто из вас готов поработать самостоятельно? Поднимите руки. Откройте тетради на печатной основе на странице 58. Рассмотрите задания № 1, 2, 3 на этой странице. – Чему будем учиться, выполняя эти задания? – Как вы думаете, какое задание более сложное? Более простое? – Выполните то задание, которое вам более интересно. (на это задание даётся 2 минуты)- Поднимите руки те, кто выполнил задание №1. Давайте проверим. Оцените ответы с помощью сигнальных карточек. (один ученик говорит, остальные показывают карточки: зелёный сигнал – согласен, красный – не согласен) – Поднимите руки те, кто выполнил задание №2, 3. (проводится аналогичная работа) – Да. Число 25 при счёте называют позже, чем 12, поэтому оно большее. – Поупражняться. Выполняют задание №3. Рекомендуемая форма ответа « 19 больше 13, т. при счёте 19 называют позже 13 и т. », « 11 меньше 14, т. при счёте 11 называют раньше 14» – Маша собрала 15 огурцов. Петя собрал 18 огурцов. Кто набрал огурцов больше: Петя или Маша? Петя собрал огурцов больше. 18 больше 15, т. его при счёте называют позже. Выполняют задание. Записывают « 17 марта. Классная работа» – 1 и 7 (прописывают по строчке цифру 1,7)Решают. Выполняют взаимопроверку. – Наибольшее число – 14, наименьшее – 11. – Наибольшее – 8, наименьшее – 6. Работают индивидуально в карточках. Осуществляют самопроверку. Поднимают руки. – Совершенствовать умение сравнивать числа. Поднимают руки. Открывают и рассматривают. – Сравнивать числа. Ответы детей. Выполняют задания по выбору. Самостоятельная работа с коллективной проверкой. Регулятивные УУД:развивать умение оценивать учебные действия в соответствии с поставленной задачей. Познавательные УУД:развиваем умения извлекать информацию из алгоритма, разворота учебника. Коммуникативные УУД:развиваем умение работать в паре. Личностные УУД: проявлять способность к самооценке на основе критерия успешности учебной деятельности, уважительное отношение к собеседнику. Регулятивные УУД:развитие самооценки 4. Рефлексия. Цель: осознание учащимися своей учебной деятельности, самооценка результатов деятельности своей и класса. – Итак, ребята, урок подходит к концу, давайте подведём его итоги. Какую учебную задачу ставили в начале урока? Удалось её решить? Чему мы научились? Вспомните, какие выводы мы делали на уроке? Сформулируйте правило сравнения чисел. – Что понравилось на уроке? Какие задания показались сложными? Оцените работу класса в целом, свою работу на уроке – закрасьте соответствующий кружок в еженедельниках. – А теперь покажите мне, пожалуйста, с каким настроением вы заканчиваете урок. – Все старались и работали на уроке хорошо. Молодцы! Спасибо вам за работу. Урок окончен. – Узнать способы сравнения чисел. – Сравнивать числа Дети отвечают правило. Ответы детей. Оценивают свою работу и работу класса в целом. Показывают карточки – смайлики. Коммуникативные УУД:развивать умение строить речевые высказывания. Регулятивные УУД:развивать умение осуществлять познавательную и личностную рефлексию.

Сохранить у себя:

Конспект урока математики “Сравнение чисел” в контексте ФГОС НОО (112 KB)

Про урокцифры: КАКАЯ ПОГОДА САМАЯ ВЕРОЯТНАЯ У ЯНДЕКС И ГУГЛ В ПРОГНОЗЕ ПОГОДЫ